Tissue Engineering Research Thrusts
Mechanical Characterization of Soft Tissues and Tissue Engineered Scaffolds
It is often required that the mechanical properties of engineered tissue match that of native biological tissue. A novel theory proposes a 3-parameter model to characterize soft tissue behavior, where the parameters are physically intuitive and are meant to assist Tissue Engineers design mechanically biomimetic scaffolds. This theory uses a unique strain decomposition to describe any arbitrary 3D strain using 3 modes: Dilation, Squeeze, and Shear. εcrimp max
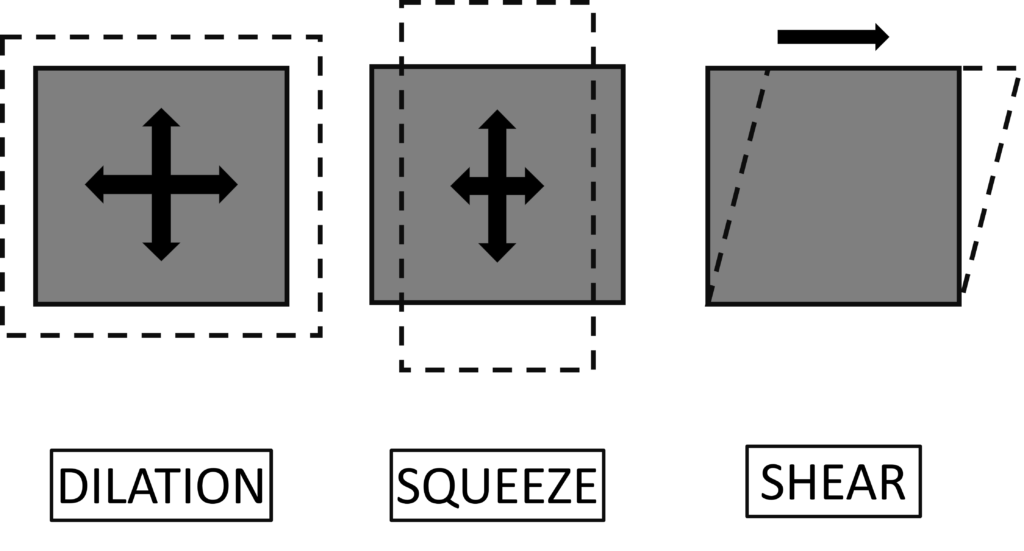
3 modes of deformation demonstrated for a 2D membrane
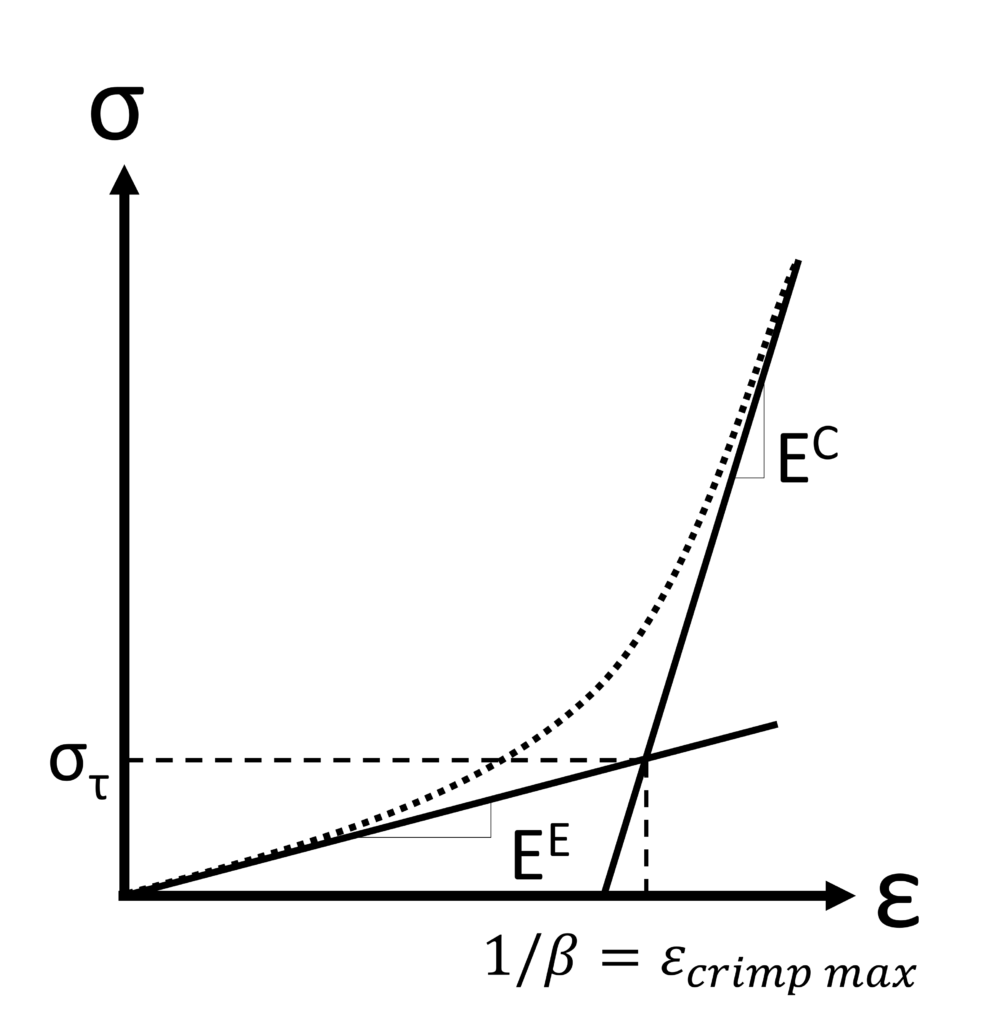
Characteristic stress-strain curve for soft tissues with an initial stiffness (EE), transitional strain (εcrimp max), and terminal stiffness (EC)
A novel biaxial system developed by the Biomechanical Environments Laboratories (BMEL) is capable of performing all three modes of deformation on a membrane, along with capturing overhead images for Digital Image Correlation.

3D Printing Tissue Scaffolds
3D printing allows fine control over scaffold architecture. BMEL uses the envisionTEC 3D-bioplotter and the Hyrel Engine HR 3D to print tissue scaffolds. Fine control over scaffold architecture allows tuning of mechanical properties.

Computer generated pattern printed using Polylactic Acid filament by generating custom g-code.
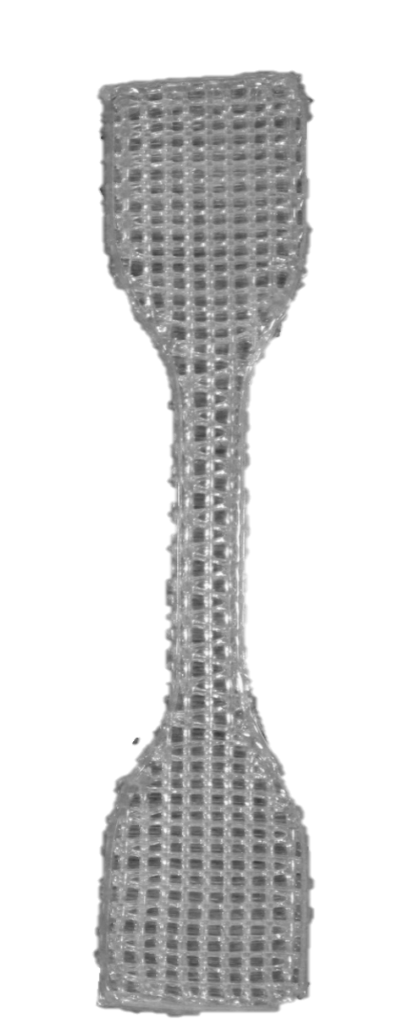
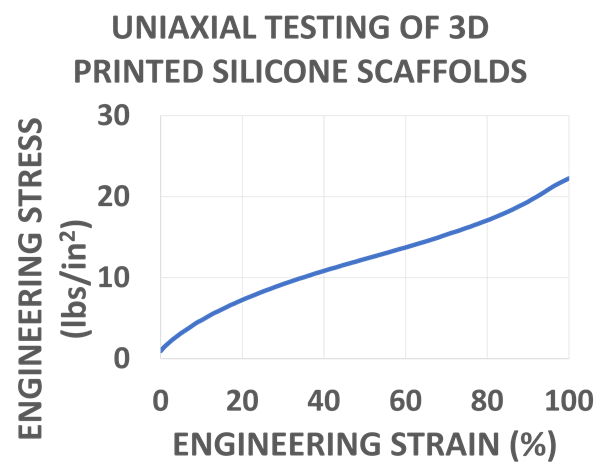
3D printed silicone scaffold (left) and the Stress-Strain curve from uniaxial tensile testing (right)
Bioreactors and cell response in Tissue Scaffolds
Biological cells are mechanotransducers i.e they react biochemically to mechanical stimuli. BMEL designs custom bioreactors that can mechanically stimulate cell-seeded scaffolds and study the cell response to different mechanical environments and the mechanical properties of the scaffold.

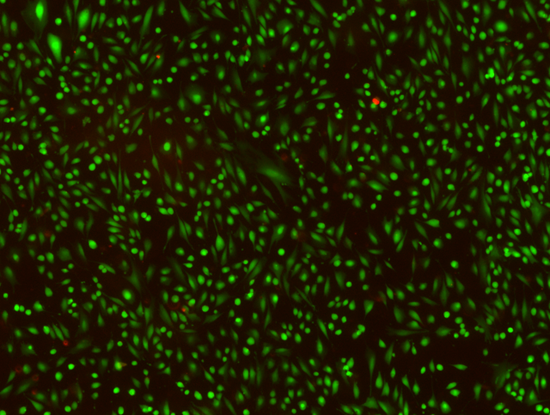
Live/dead assay performed on 3T3 fibroblasts stretched on PDMS membrane show good cell viability
(Green – Live, Red – Dead)
